Groupwise registration formulation
The objective of groupwise registration is to concurrently align all cine photos to a typical reference body. Let (:textual content{f}left(mathbf{x},textual content{t}proper)) signify the cine picture sequence, the place the spatial coordinate (:mathbf{x}in:{Omega:}=left{left(textual content{x},textual content{y}proper)proper|1le:textual content{x}le:{textual content{N}}_{textual content{x}},1le:textual content{y}le:{textual content{N}}_{textual content{y}}}) and the temporal coordinate (:1le:textual content{t}le:{textual content{N}}_{textual content{t}}). (:{textual content{N}}_{textual content{x}}), (:{textual content{N}}_{textual content{y}}), and (:{textual content{N}}_{textual content{t}}) signify the pixel quantity within the x path, pixel quantity within the y path, and body quantity, respectively. The deformed cine picture sequence might be expressed as
$$:stackrel{sim}{textual content{f}}left(mathbf{x},textual content{t}proper)=textual content{f}left(mathbf{T}left(mathbf{x},textual content{t}proper),textual content{t}proper)=textual content{f}left(mathbf{x}+mathbf{d}left(mathbf{x},textual content{t}proper),textual content{t}proper),$$
(1)
the place (:mathbf{T}left(mathbf{x},textual content{t}proper)=mathbf{x}+mathbf{d}left(mathbf{x},textual content{t}proper)) is the transformation area and (:mathbf{d}left(mathbf{x},textual content{t}proper)) is the displacement area. We use the free-form deformation modeling of the displacement area [24]. Particularly, given a management level mesh (bf{Phi} ({rm{i}},{rm{j}},{rm{t}})) with uniform management level spacing (:{updelta:}), (:mathbf{d}left(mathbf{x},textual content{t}proper)) is modeled by a linear mixture of management factors with cubic B-spline coefficients as
$${bf{d}}left( {{bf{x}},{rm{t}}} proper) = sumlimits_{{rm{okay}} = 0}^3 {} sumlimits_{{rm{l}} = 0}^3 {{{rm{B}}_{rm{okay}}}left( {rm{u}} proper){{rm{B}}_{rm{l}}}left( {rm{v}} proper)bf{Phi} left( {{rm{i}} + {rm{okay}},{rm{j}} + {rm{l}},{rm{t}}} proper)} ,$$
(2)
the place (:textual content{i}=lfloor:(textual content{x}-1)/{updelta:}rfloor,:) (:textual content{j}=lfloor:(textual content{y}-1)/{updelta:}rfloor:), (:textual content{u}=(textual content{x}-1)/{updelta:}-lfloor:(textual content{x}-1)/{updelta:}rfloor:), (:textual content{v}=(textual content{y}-1)/{updelta:}-lfloor:(textual content{y}-1)/{updelta:}rfloor:), and (:{textual content{B}}_{textual content{okay}}left(textual content{u}proper)) is the (:textual content{okay})-th foundation perform of the B-splines. By constraining the temporal common of the transformation or displacement area to be an identification map or zero, we register all photos to a mean widespread reference body:
$${1 over {{{rm{N}}_{rm{t}}}}}sumlimits_{{rm{t}} = 1}^{{{rm{N}}_{rm{t}}}} {{bf{T}}({bf{x}},{rm{t}}) = {bf{x}}>> Leftrightarrow } >>{1 over {{{rm{N}}_{rm{t}}}}}sumlimits_{{rm{t}} = 1}^{{{rm{N}}_{rm{t}}}} {{bf{d}}({bf{x}},{rm{t}}) = 0,}$$
(3)
Which primarily based on Eq. (2) is equal to
$${1 over {{{rm{N}}_{rm{t}}}}}sumlimits_{{rm{t}} = 1}^{{{rm{N}}_{rm{t}}}} {bf{Phi} ({rm{i}},{rm{j}},{rm{t}}) = 0.}$$
(4)
GLR and LLR dissimilarity metrics
To register all photos in (:stackrel{sim}{textual content{f}}left(mathbf{x},textual content{t}proper)), we are able to use both the beforehand described GLR metric [18, 19] or the proposed LLR metric. To make use of the GLR metric, one firstly reformulates your complete sequence of photos right into a Casorati matrix:
$$bf {rm{bf{C}}} = left[ {matrix{{{rm{tilde f}}left( {{{rm{bf{x}}}_{rm{1}}}{rm{,1}}} right)} & {{rm{tilde f}}left( {{{rm{bf{x}}}_{rm{1}}}{rm{,2}}} right)} & cdots & {{rm{tilde f}}left( {{{rm{bf{x}}}_{rm{1}}}{rm{,}}{{rm{N}}_{rm{t}}}} right)} cr {{rm{tilde f}}left( {{{rm{bf{x}}}_{rm{2}}}{rm{,1}}} right)} & {{rm{tilde f}}left( {{{rm{bf{x}}}_{rm{2}}}{rm{,2}}} right)} & cdots & {{rm{tilde f}}left( {{{rm{bf{x}}}_{rm{2}}}{rm{,}}{{rm{N}}_{rm{t}}}} right)} cr vdots & vdots & ddots & vdots cr {{rm{tilde f}}left( {{{rm{bf{x}}}_{rm{L}}}{rm{,1}}} right)} & {{rm{tilde f}}left( {{{rm{bf{x}}}_{rm{L}}}{rm{,2}}} right)} & cdots & {{rm{tilde f}}left( {{{rm{bf{x}}}_{rm{L}}}{rm{,}}{{rm{N}}_{rm{t}}}} right)} cr } } right] in >{mathbb{R}^{{rm{L instances }}{{rm{N}}_{rm{t}}}}},$$
(5)
the place (:textual content{L}={textual content{N}}_{textual content{x}}{textual content{N}}_{textual content{y}}) is the overall variety of voxels, and the (:textual content{l})-th row holds the sign within the (:textual content{l})-th voxel. GLR assumes the Casorati matrix is rank-deficient if all photos are properly aligned. The GLR dissimilarity is thus decided by the nuclear norm of (:mathbf{C}):
$${{rm{D}}_{{rm{GLR}}}} = parallel{bf{C}}{parallel _{rm{*}}} = sumlimits_{{rm{t}} = 1}^{{{rm{N}}_{rm{t}}}} {{{rm{sigma }}_{rm{t}}},}$$
(6)
the place (:{{upsigma:}}_{textual content{t}}) is the (:textual content{t})-th singular worth of (:mathbf{C}).
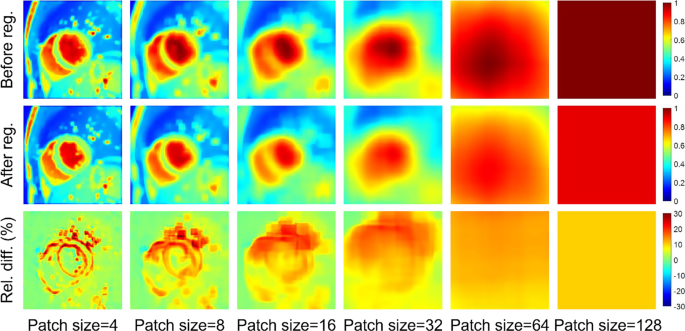
In cardiac cine imaging, nonetheless, alerts could also be spatially inconsistent even after registration, attributable to a set of confounders equivalent to movement, blood circulate, and artifacts. Because of this, the post-registration international rank could also be nonetheless excessive, rendering GLR much less efficient for the steering of the registration. Determine 1 illustrates this downside utilizing a practical cine film instance. From the illustration, it’s clear that the native sign rank is extra delicate to the elimination of movement than the worldwide sign rank. For instance, the rank for voxels surrounding the myocardium border is decreased considerably by the registration. Subsequently, we suggest to make use of the LLR metric, which uniformly partitions the spatial area into (:{textual content{N}}_{textual content{c}}) overlapped sq. patches with a prespecified patch measurement and spacing, reformulates the patches into native Casorati matrices, and computes the sum of the nuclear norm of those native Casorati matrices:
$${{rm{D}}_{{rm{LLR}}}} = sumlimits_{{rm{okay = 1}}}^{{{rm{N}}_{rm{c}}}} {parallel {{bf{C}}_{rm{okay}}}{parallel _{rm{*}}} = } sumlimits_{{rm{okay = 1}}}^{{{rm{N}}_{rm{c}}}} {} sumlimits_{{rm{t = 1}}}^{{{rm{N}}_{rm{t}}}} {{{rm{sigma }}_{{rm{okay,t}}}}} ,$$
(7)
the place (:{bf{C}}_{rm{okay}}) is the native Casorati matrix related to the (:textual content{okay})-th patch, and (:{rm{sigma }}_{{rm{okay,t}}}) is the (:textual content{t})-th singular worth of (:{bf{C}}_{rm{okay}}).
The maps of LLR price—a surrogate of the patchwise sign rank—of a cine picture sequence within the ACDC dataset earlier than (Row 1) and after (Row 2) registration. Row 3 exhibits the relative distinction between Row 1 and Row 2. Word that the rank discount is extremely region-dependent, with excessive reductions (~ 40%) in areas with giant movement, such because the myocardial borders. Some areas have a excessive rank even after picture registration, such because the blood pool. GLR, which is equal to LLR with a patch measurement of 128 (the rightmost column), assumes the rank is globally low after picture registration. Nevertheless, because the rightmost column exhibits, the post-registration international rank continues to be excessive, leading to solely a ~ 10% rank discount
Regularization
To implement the spatiotemporal regularity of the deformation area, we use a mix of spatial and temporal regularization phrases. For the spatial smoothness, we introduce a bending-energy-based regularization time period over the spatial area [24]:
$$eqalign{{{rm{R}}_{{rm{spatial}}}} & = sumlimits_{{rm{t}} = 1}^{{{rm{N}}_{rm{t}}}} {} sumlimits_{{bf{x}} in >Omega } {} left| {{{partial {>^2}{bf{T}}} over {partial >{{rm{x}}^2}}}({bf{x}},{rm{t}})} proper|_2^2 cr & + 2left| {{{partial {>^2}{bf{T}}} over {partial >{rm{x}}partial >{rm{y}}}}({bf{x}},{rm{t}})} proper|_2^2 + left| {{{partial {>^2}{bf{T}}} over {partial >{{rm{y}}^2}}}({bf{x}},{rm{t}})} proper|_2^2. cr}$$
(8)
For the temporal smoothness, we introduce a second-order regularization time period over the temporal area
$${{rm{R}}_{{rm{temporal}}}} = sumlimits_{{rm{t}} = 1}^{{{rm{N}}_{rm{t}}}} {} sumlimits_{{bf{x}} in >Omega } {} left| {{{partial {>^2}{bf{T}}} over {partial >{{rm{t}}^2}}}({bf{x}},{rm{t}})} proper|_2^2.$$
(9)
We approximate the partial derivates in (:{textual content{R}}_{textual content{s}textual content{p}textual content{a}textual content{t}textual content{i}textual content{a}textual content{l}}) and (:{textual content{R}}_{textual content{t}textual content{e}textual content{m}textual content{p}textual content{o}textual content{r}textual content{a}textual content{l}}) by the finite variations. Moreover, given the cyclic movement of the guts, we undertake cyclic finite variations in (:{textual content{R}}_{textual content{t}textual content{e}textual content{m}textual content{p}textual content{o}textual content{r}textual content{a}textual content{l}}) to implement the consistency of the movement between the primary body and the final body.
Because of this, the proposed LLR-based groupwise registration (Groupwise-LLR) is formulated as
$$start{aligned}:underset{varvec{upvarphi:}}{textual content{min}}{textual content{D}}_{textual content{L}textual content{L}textual content{R}} & +{uplambda:}{textual content{R}}_{textual content{s}textual content{p}textual content{a}textual content{t}textual content{i}textual content{a}textual content{l}}+{upmu:}{textual content{R}}_{textual content{t}textual content{e}textual content{m}textual content{p}textual content{o}textual content{r}textual content{a}textual content{l}} & quad textual content{s}.textual content{t}.frac{1}{{textual content{N}}_{textual content{t}}}sum:_{textual content{t}=1}^{{textual content{N}}_{textual content{t}}}varvec{upvarphi:}(textual content{i},textual content{j},textual content{t})=0,finish{aligned}$$
(10)
the place (:{uplambda:}) and (:{upmu:}) are the regularization coefficients, and the constraint is from Eq. 4. Impressed by a earlier examine on groupwise registration [25], we applied the projected gradient descent algorithm to unravel this downside in a coarse-to-fine multi-resolution framework. On this framework, the proposed methodology firstly estimates the deformation on the lowest decision stage to roughly align the photographs. Then, the tactic step by step refines the deformation at increased decision ranges to attain extra correct alignment. We initialize the management level mesh (bf{Phi} ({rm{i}},{rm{j}},{rm{t}})) as zero, resulting in zero displacements throughout all cardiac phases.
Pressure estimation
After acquiring the temporally resolved transformation area, we estimate the transformation area from the primary picture (end-diastole) to every later picture by a two-step course of, through which the coordinate (:mathbf{x}) within the end-diastolic picture is firstly mapped to the widespread reference body, after which to the (:textual content{t})-th picture. Mathematically, this course of is represented by
$${{bf{T}}_{1 to {rm{t}}}}left( {bf{x}} proper) = {bf{T}}left( {{{bf{T}}^{ – 1}}left( {{bf{x}},1} proper),{rm{t}}} proper),$$
(11)
the place ({{bf{T}}_{1 to {rm{t}}}}left( {bf{x}} proper)) represents the transformation area from the primary picture to the (:textual content{t})-th picture. Primarily based on the estimated ({{bf{T}}_{1 to {rm{t}}}}left( {bf{x}} proper)), the Inexperienced-Lagrange pressure tensor [26] is evaluated by
$${bf{E}}left( {{bf{x}},{rm{t}}} proper) = {1 over 2}left[ {{{left( {nabla {>_{bf{x}}}{{bf{T}}_{1 to {rm{t}}}}left( {bf{x}} right)} right)}^{rm{T}}}nabla {>_{bf{x}}}{{bf{T}}_{1 to {rm{t}}}}left( {bf{x}} right) – {bf{I}}} right],$$
(12)
the place (:{nabla:}_{mathbf{x}}) represents the Jacobian operator about (:mathbf{x}) (applied utilizing finite variations) and (:mathbf{I}) is an identification matrix of measurement two. The pressure alongside a sure path is then computed by
$$:{textual content{e}}_{mathbf{u}}left(mathbf{x},textual content{t}proper)={left(mathbf{u}left(mathbf{x}proper)proper)}^{textual content{T}}mathbf{E}left(mathbf{x},textual content{t}proper)mathbf{u}left(mathbf{x}proper),$$
(13)
the place (:mathbf{u}left(mathbf{x}proper)) is the pressure path area decided by segmentation of the left ventricular myocardium within the end-diastolic picture. For these long-axis slices, (:mathbf{u}left(mathbf{x}proper)) represents the longitudinal path; for these short-axis slices, (:mathbf{u}left(mathbf{x}proper)) represents the circumferential or radial path. The worldwide longitudinal pressure (GLS) is estimated by averaging the pressure values over the left ventricular myocardium inside a single long-axis slice. The worldwide circumferential pressure (GCS) and international radial pressure (GRS) are estimated by averaging the pressure values over the left ventricular myocardium inside a specified slice (e.g., base, mid-ventricle, apex) or throughout a number of slices overlaying your complete left ventricle.
Baseline strategies
The proposed Groupwise-LLR was in contrast with the Farneback optical circulate [27], a commercially out there pairwise registration methodology [28], and the GLR-based groupwise registration (Groupwise-GLR) primarily based on each simulated and in-vivo information. Amongst these different CMR-FT strategies, the optical circulate and pairwise registration estimate the transformation area between every pair of the neighboring photos, i.e., ({{bf{T}}_{{rm{t}} – 1 to {rm{t}}}}left( {bf{x}} proper)), (:2le:textual content{t}le:{textual content{N}}_{textual content{t}}). The transformation area ({{bf{T}}_{1 to {rm{t}}}}left( {bf{x}} proper)) is then a composition of the neighboring transformation fields. Groupwise-GLR was applied in the identical method as Groupwise-LLR aside from using a GLR dissimilarity metric. The proposed methodology was additionally in contrast with two common groupwise registration strategies, nD+t B-Splines [16] and pTVreg [21], in simulations and in vivo monitoring. Amongst them, nD + t B-Splines makes use of an nD + t B-spline deformation mannequin and a sum of the voxelwise sign variances because the dissimilarity metric. pTVreg makes use of the same LLR metric because the proposed one. Nevertheless, pTVreg extracts nonoverlapped patches to compute the LLR metric and fixes the patch measurement for all decision ranges. As compared, Groupwise-LLR partitions the spatial area into overlapped patches to boost the continuity of the estimated movement amongst neighboring patches, and adjusts the patch measurement together with the picture decision to enhance the consistency of the multi-resolution optimization. Moreover, pTVreg is characterised by the overall variation regularization, which is completely different from the second-order Tikhonov regularization used on this work. Moreover, it needs to be emphasised that the proposed Groupwise-LLR is the primary pressure estimation methodology primarily based on groupwise registration whereas the 2 baseline groupwise registration strategies haven’t been utilized for pressure estimation earlier than.
Implementation particulars
All strategies had been applied with MATLAB (R2022a, MathWorks, Natick, MA, USA). The parameters of every methodology had been manually tuned for the simulated and in vivo experiments. For the proposed Groupwise-LLR, the variety of decision ranges was 3 and the downsampling issue between two adjoining decision ranges was 2. The regularization coefficients weren’t reweighted between completely different decision ranges. The cubic interpolation was used for picture downsampling and the linear interpolation was used for picture warping. The patch measurement and spacing used to pattern the native Casorati matrices had been 5 and three pixels on the lowest decision stage and doubled every time transferring to the subsequent stage. The management level spacing, spatial regularization coefficient (:{uplambda:}), and temporal regularization coefficient (:mu:) had been 6 and seven pixels, 6х10− 4 and 1х10− 3, 0.06 and 0.1 for the simulated dataset and two in vivo datasets, respectively. We decided the regularization coefficients utilizing a semi-quantitative method primarily based on small separate trial datasets. For the simulated experiments, we firstly set (:{uplambda:}) = 5х10− 4 primarily based on a guide inspection of the spatial smoothness of the displacement fields. We then various the ratio (:mu:/{uplambda:}) from 0.1 to 1000, and located that (:mu:/{uplambda:}) = 100 minimized the EPE over the simulated trial dataset. Thus, we fastened (:mu:/{uplambda:}) = 100 hereafter. We various (:{uplambda:}) from 2х10− 4 to 1х10− 3 with a step of 2х10− 4, and located that (:{uplambda:}) = 6х10− 4 minimized the EPE over the simulated trial dataset. For the in-vivo experiments, we tried completely different values of (:{uplambda:}) from 5х10− 4 to 2.5х10− 3 with a step of 5х10− 4, and located that (:{uplambda:}) = 1х10− 3 minimized the imply contour distances over the in-vivo trial dataset. The optimization at every decision stage was terminated when the relative worth change of the associated fee perform was lower than a tolerance of 1х10− 5.
Simulations
The simulated cine MRI dataset was generated by a digital phantom (XCAT) [22] and its MRI extension MRXCAT [29]. Particularly, XCAT was used to generate the cardiac-phase-resolved 3D tissue masks of 20 topics, every with a special gender, cardiac anatomy, and cardiac movement sample. The corresponding transformation area was additionally generated for every topic. Interpolation was then used to generate 2D cine films in a 2-chamber slice and seven or 8 short-axis slices, with a 1.5 mmх1.5 mm decision and 24 frames. MRXCAT was then used to generate the sign depth of every tissue in cine MRI. The studied function monitoring strategies had been carried out in every slice to estimate the strains. The monitoring high quality was evaluated by end-point error (EPE), which is the distinction between the estimated transformation area and its floor fact, averaged over your complete myocardium at end-systole or over your complete cardiac cycle. Pressure error was computed at end-systole for each voxelwise (VSE) and international (GSE) ranges, the place the previous was a mean of absolute pressure distinction between the estimated pressure and floor fact over your complete myocardium, and the latter was absolutely the distinction between the worldwide estimated pressure and international floor fact pressure.
Experiments on the ACDC dataset
The ACDC dataset [23] incorporates 100 topics evenly distributed over 5 examine teams: dilated cardiomyopathy (DCM), myocardial infarction (MI), irregular proper ventricle (ARV), hypertrophic cardiomyopathy (HCM), and regular cardiac anatomy and performance (NOR). For every topic, a sequence of short-axis cine photos had been acquired with a balanced steady-state free-precession (bSSFP) sequence on a 1.5T (Siemens Space, Siemens Medical Options, Germany) or 3T (Siemens Trio Tim, Siemens Medical Options, Germany) medical scanner. Handbook segmentation of the end-diastolic and end-systolic myocardium is supplied by the dataset. To guage the monitoring accuracy of a technique, the end-diastolic epicardial and endocardial contours had been first tracked to the end-systolic section. Then, the imply distance between the tracked and annotated end-systolic contours was computed within the basal, mid-ventricular, and apical slices. To guage the inter-observer reproducibility of the measured strains, the end-diastolic endocardium and epicardium had been independently contoured by a reader (3 years of cardiac MR expertise) in a subset (n = 30) of the ACDC dataset, and the intraclass correlation coefficients (ICC) of the end-systolic international strains (radial and circumferential) primarily based on the annotations by the dataset and the reader had been calculated. To guage the intra-observer reproducibility, the identical set of information was annotated by the identical reader over one yr later, and the ICC primarily based on the 2 annotations by this reader had been calculated.
Experiments on the affected person dataset
The affected person examine was permitted by the institutional assessment board. All sufferers supplied knowledgeable written consent. The medical dataset incorporates 16 sufferers (9 male, age 51 ± 14 years) scanned between February 2016 and February 2017 on a 3T scanner (Philips Ingenia Elition, Philips Healthcare, Nederland). Scientific indications included regular (n = 3), coronary coronary heart illnesses (n = 4), connective tissue illnesses (n = 4), nonischemic coronary heart illnesses (n = 3), and different (n = 2). All sufferers had been scanned with a bSSFP cine sequence and a tagging-MRI sequence. The bSSFP cine sequence used the next parameters: TR = 2.8 ms, TE = 1.4 ms, bandwidth = 1890 Hz/pixel, flip angle = 45°, FOV = 268х280 mm2, matrix measurement = 134х140, slice thickness = 7 mm, variety of phases = 30. The tagging-MRI sequence had the next parameters: TR = 5.9 ms, TE = 3.6 ms, bandwidth = 432 Hz/pixel, flip angle = 10°, tag spacing = 7 mm, FOV = 229х280 mm2, matrix measurement = 154х188, slice thickness = 8 mm, variety of phases = 9 to16. For every topic, solely the matched cine and tagging photos at basal, mid-ventricular, and apical short-axis slices had been analyzed. The left ventricular myocardium in every end-diastolic cine or tagging picture was annotated in response to the AHA 16-segment mannequin [30]. The tagging photos had been analyzed by pairwise registration following a earlier work [31]. The top-systolic international and segmental strains estimated by the CMR-FT strategies had been in contrast with these by tagging utilizing ICC.
Statistics
Steady variables had been reported as imply ± normal deviation. The Wilcoxon signed rank take a look at was carried out to find out whether or not two steady variables had been equal. The impact measurement of the Wilcoxon signed rank take a look at was computed by dividing absolutely the standardized take a look at statistic z by the sq. root of the variety of pattern pairs. Following Cohen’s classification [32], the brink of the impact measurement for a small, medium, and enormous impact are 0.1, 0.3, and 0.5, respectively. For analysis of the inter/intra-observer reproducibility, ICC was calculated utilizing a single score, absolute settlement, and 2-way mixed-effects mannequin; for analysis of the cine-tagging correlation, ICC was calculated utilizing a single score, consistency, and 2-way mixed-effects mannequin [33]. Bland-Altman evaluation was additionally carried out to guage the inter/intra-observer reproducibility of every methodology. All statistical analyses had been carried out with MATLAB and SPSS (Model 26, IBM, New York, USA). P values lower than 0.05 had been thought of statistically important.